Индикатор области баланса при выборе параметра
в методе регуляризации Тихонова
А.М. Соколов
Институт ядерных исследований НАН Украины, Киев
Учет искажающего влияния аппаратуры при регистрации экспериментальных данных приводит к решению интегрального уравнения Фредгольма 1-го рода:
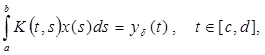 (в операторном виде Kx = yδ)
, (1)
(в операторном виде Kx = yδ)
, (1)
где x(s) – интересующая нас исходная зависимость (неискаженный спектр), yδ(t) – полученная в результате регистрации спектра аппаратурой зависимость (зарегистрированный спектр), δ-уровень ее погрешности, K(t,s) – аппаратная функция, предполагаемая заданной.
На решение уравнения (1) сильно влияет погрешность в правой части. Поэтому в методе регуляризации Тихонова уравнение (1) заменяется задачей на минимум сглаживающего функционала:
![]() .
(2)
.
(2)
Решение задачи (2), т.е. функция xα , зависит от параметра регуляризации (ПР) α, балансирующего требования к частям функционала в (2). Важно удачно выбрать α.
Введем параметрические функционалы (функции от параметра α):
![]() и
и ![]() . (3)
. (3)
 Основные их
свойства хорошо изучены [2]. Обе функции строго монотонны. Функция
Основные их
свойства хорошо изучены [2]. Обе функции строго монотонны. Функция ![]() (невязка уравнения (1) на xα) возрастает,
норма регуляризованного решения
(невязка уравнения (1) на xα) возрастает,
норма регуляризованного решения ![]() убывает. На
основе
убывает. На
основе ![]() строится критерий выбора ПР по
принципу невязки [2]. Мы будем использовать для выявления условия баланса
функцию нормы регуляризованного решения. Для этого сравним значения функции γ(α)
для двух разных значений параметра регуляризации, например, для α и q·α , где q > 1. Удобно
взять параметр q = 10 , т.е. изменить α на один порядок.
В качестве индикатора возьмем отношение
строится критерий выбора ПР по
принципу невязки [2]. Мы будем использовать для выявления условия баланса
функцию нормы регуляризованного решения. Для этого сравним значения функции γ(α)
для двух разных значений параметра регуляризации, например, для α и q·α , где q > 1. Удобно
взять параметр q = 10 , т.е. изменить α на один порядок.
В качестве индикатора возьмем отношение
![]() , (4)
, (4)
Из строгой монотонности убывающей функции ![]() следует,
что
следует,
что ![]() . Кроме того, оказывается
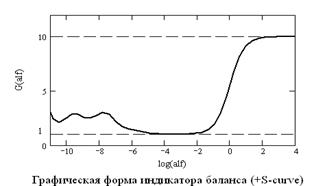
. Кроме того, оказывается ![]() . В области баланса график функции G(α), с
логарифмической шкалой по α, имеет хорошо выраженный широкий минимум, где значения
G(α) близки к 1. Область
минимума G(α) соответствует
области баланса для ПР в (2). С ростом параметра α функция возрастает,
приближаясь к значению q. Поэтому правая часть графика G(α) имеет
характерную S–образную форму.
. В области баланса график функции G(α), с
логарифмической шкалой по α, имеет хорошо выраженный широкий минимум, где значения
G(α) близки к 1. Область
минимума G(α) соответствует
области баланса для ПР в (2). С ростом параметра α функция возрастает,
приближаясь к значению q. Поэтому правая часть графика G(α) имеет
характерную S–образную форму.
1. А.Н. Тихонов, В.Я. Арсенин. Методы решения некорректных задач. -М.: Наука, 1979.
2. В.А. Морозов. Регулярные методы решения некорректно поставленных задач. - М.: изд. МГУ, 1974.